미적분

수열의 극한

수열의 수렴과 발산

Definition 1 (수열의 수렴) 수열 ${a_{n}}$ 에서 $a_{n}$ 이 한없이 커질때, $a_{n}$ 의 값이 일정한 값 $α$ 에 한없이 가까워지면 수열 ${a_{n}}$ 은 $α$ 에 수렴한다고 한다. 이때 $α$ 를 수열 ${a_{n}}$ 의 극한값 또는 극한이라 하고, 이것을 기호로 $lim_{n \to \infty} a_{n} = α$ 또는 $n \to \infty \Rightarrow a_{n} \to α$ 와 같이 나타낸다.

Definition 2 (수열의 발산) 수열 ${a_{n}}$ 이 수렴하지 않을 때, 이 수열은 발산한다고 한다.

Remark (remark-수열의 발산). 수열 ${a_{n}}$ 이 발산하는 경우는 아래의 3가지 경우로 나눌 수 있다.

양의 무한대로 발산

$lim_{n \to \infty} a_{n} = \infty 또는 n \to \infty \Rightarrow a_{n} \to \infty$

음의 무한대로 발산

$lim_{n \to \infty} a_{n} = - \infty 또는 n \to \infty \Rightarrow a_{n} \to - \infty$

진동

수열 ${a_{n}}$ 이 수렴하지도 않고 양의 무한대나 음의 무한대로 발산하지도 않으면 수열 ${a_{n}}$ 은 진동한다고 한다.

수열의 극한에 대한 기본 성질

Theorem 1 (수열의 극한에 대한 기본 정리) 두 수열 ${a_{n}}$ , ${a_{n}}$ 이 수렴하고 $lim_{n \to \infty} a_{n} = α$ , $lim_{n \to \infty} b_{n} = β$ ( $α, β$ 는 실수) 일 때, 다음이 성립한다. $\begin{aligned} lim_{n \to \infty} (a_{n} + b_{n}) & = lim_{n \to \infty} a_{n} + lim_{n \to \infty} b_{n} \\ lim_{n \to \infty} (a_{n} - b_{n}) & = lim_{n \to \infty} a_{n} - lim_{n \to \infty} b_{n} \\ lim_{n \to \infty} (c \cdot a_{n}) & = c \cdot lim_{n \to \infty} a_{n} w h e r e c i s c o n s t a n t \\ lim_{n \to \infty} (a_{n} \cdot b_{n}) & = lim_{n \to \infty} a_{n} \cdot lim_{n \to \infty} b_{n} \\ lim_{n \to \infty} (a_{n} / b_{n}) & = lim_{n \to \infty} a_{n} / lim_{n \to \infty} b_{n} w h e r e b_{n} \neq 0 \land lim_{n \to \infty} b_{n} \neq 0 \end{aligned}$

수열의 극한값의 계산

수열의 극한값의 대소 관계

Theorem 2 (수열의극한의대소관계) ${a_{n}}$ , ${b_{n}}$ , ${c_{n}}$ 이 각각 수열이다. 두 수열 ${a_{n}}$ , ${a_{n}}$ 이 수렴하고 $lim_{n \to \infty} a_{n} = α$ , $lim_{n \to \infty} b_{n} = β$ ( $α, β$ 는 실수)일 때, 다음이 성립한다. $\begin{aligned} (\forall n \in N) & (a_{n} \leq b_{n} \to α \leq β) \\ (\forall n \in N) & (a_{n} \leq c_{n} \leq b_{n} \land α = β \to lim_{n \to \infty} c_{n} = α) \end{aligned}$

등비수열의극한

Theorem 3 (등비수열의 수렴과 발산) 초항은 $1$ , 공비는 $r$ , 즉 일반항이 $a_{n} = r^{n - 1}$ 인 등비수열 ${a_{n}}$ 은 공비 $r$ 의 값의 범위에 따라 수렴 또는 발산한다. $\begin{aligned} r > 1 & \to lim_{n \to \infty} r^{n} = \infty \\ r = 1 & \to lim_{n \to \infty} r^{n} = 1 \\ | r | < 1 & \to lim_{n \to \infty} r^{n} = 0 \\ r \leq - 1 & \to lim_{n \to \infty} r^{n} 은 진동 i.e. 발산 \end{aligned}$

Theorem 4 (등비수열의 수렴 조건) 초항은 $a$ , 공비는 $r$ , 즉 일반항이 $a_{n} = a r^{n - 1}$ 인 등비수열 ${a_{n}}$ 의 수렴 조건은 다음과 같다. $(a = 0) \lor (- 1 < r \leq 1)$

급수의 수렴과 발산

급수와 수열의 극한 사이의 관계

등비급수

급수의성질

함수의 극한과 연속

함수의 극한

함수의 수렴과 발산

우극한과 좌극한

함수의 극한에 대한 성질

함수의 극한의 응용

Definition 3 (the limit of a function) $f : D \to R$ be a function defined on a subset $D \subseteq R$ , let $a$ be a limit point of $D$ , and let $L$ be a real number. Then the function $f$ has a limit $L$ at $a$ is defined to mean for all $ε > 0$ , there exists a $δ > 0$ such that for all $x$ in $D$ that satisfy $0 < | x - a | < δ$ , the inequality $| f (x) - L | < ε$ holds.

Symbolically: $lim_{x \to a} f (x) = L ⟺ (\forall x \in D) (\forall ε > 0) (\exists δ > 0) (0 < | x - a | < δ \Rightarrow | f (x) - L | < ε)$

Definition 4 (One-sided limit, right-sided limit) $lim_{x \to a^{+}} f (x) ⟺ (\forall x \in D) (\forall ε > 0) (\exists δ > 0) (0 < x - a < δ \Rightarrow | f (x) - L | < ε)$

Definition 5 (One-sided limit, left-sided limit) $lim_{x \to a^{-}} f (x) ⟺ (\forall x \in D) (\forall ε > 0) (\exists δ > 0) (0 < a - x < δ \Rightarrow | f (x) - L | < ε)$

Theorem 5 (함수의 극한에 대한 정리) $lim_{x \to p} f (x)$ 와 $lim_{x \to p} g (x)$ 가 수렴할 때, $\begin{aligned} lim_{x \to p} (f (x) + g (x)) & = lim_{x \to p} f (x) + lim_{x \to p} g (x) \\ lim_{x \to p} (f (x) - g (x)) & = lim_{x \to p} f (x) - lim_{x \to p} g (x) \\ lim_{x \to p} (f (x) \cdot g (x)) & = lim_{x \to p} f (x) \cdot lim_{x \to p} g (x) \\ lim_{x \to p} (f (x) / g (x)) & = lim_{x \to p} f (x) / lim_{x \to p} g (x) w h e r e lim_{x \to p} g (x) \neq 0 \end{aligned}$

Theorem 6 (미정계수의 결정) $lim_{x \to a} \frac{f (x)}{g (x)} = L$ ( $L$ 은 상수) 일 때,

$\begin{matrix} (1) & \begin{aligned} lim_{x \to a} f (x) = 0 \land L \neq 0 & \Rightarrow lim_{x \to a} g (x) = 0 \\ lim_{x \to a} g (x) = 0 & \Rightarrow lim_{x \to a} f (x) = 0 \end{aligned} \end{matrix}$

이것은 referencing Equation 1 테스트 입니다.

함수의 연속

Definition 6 (Continuity) A function $f$ is said to be continuous at $c$ if it is both defined at $c$ and its value at $c$ equals the limit of $f$ as $x$ approaches $c$ . $lim_{x \to c} f (x) = f (c)$

연속함수

Theorem 7 (연속함수의 성질) 두 함수 $f (x)$ , $g (x)$ 가 $x = c$ 에서 연속이면 다음 함수도 모두 $x = c$ 에서 연속이다.

$k f (x)$ , 단 $k$ 는 상수
$f (x) \pm g (x)$
$f (x) g (x)$
$\frac{f (x)}{g (x)}$ , 단 $g (x) \neq 0$

Theorem 8 (EVT : The Maximum Minimum Theorem) $f \in C^{0} ([a, b], R) \Rightarrow (\forall x \in [a, b]) (\exists c \in [a, b]) (\exists d \in [a, b]) (f (c) \geq f (x) \land f (d) \leq f (x))$

Theorem 9 (EVT : 최대·최소 정리) 함수 $f (x)$ 가 닫힌구간 $[a, b]$ 에서 연속이면 $f (x)$ 는 이 구간에서 반드시 최댓값과 최솟값을 갖는다.

사잇값 정리

Theorem 10 (IVT : The intermediate value theorem) $f \in C^{0} ([a, b], R) \land f (a) \neq f (b) \Rightarrow (\forall k \in (| f (a), f (b) |)) (\exists c \in (a, b)) (f (c) = k)$

Theorem 11 (사잇값정리) 함수 $f (x)$ 가 닫힌구간 $[a, b]$ 에서 연속이고, $f (a) \neq f (b)$ 이면 $f (a)$ 와 $f (b)$ 사이의 임의의 실수 $k$ 에 대하여 $f (c) = k$ 인 $c$ 가 열린 구간 $(a, b)$ 에 적어도 하나 존재한다.

Corollary 1 (Bolzano’s theorem) $(f \in C^{0} ([a, b], R) \land (f (a) f (b) < 0)) \Rightarrow (\exists c \in (a, b)) (f (c) = 0)$

Corollary 2 (사잇값 정리의 활용) 함수 $f (x)$ 가 닫힌구간 $[a, b]$ 에서 연속이고, $f (a) f (b) < 0$ 이면 방정식 $f (x) = 0$ 은 열린 구간 $(a, b)$ 에서 적어도 하나의 실근을 갖는다.

미분

미분계수와 도함수

평균변화율과 미분계수

Definition 7 (증분) 함수 $y = f (x)$ 에서 $x$ 의 값이 $a$ 에서 $b$ 까지 변할 때, $y$ 의 값은 $f (a)$ 에서 $f (b)$ 까지 변한다. 이 때 $x$ 의 값의 변화량 $b - a$ 를 $x$ 의 증분, $y$ 의 값의 변화량 $f (b) - f (a)$ 를 $y$ 의 증분이라 하고, 기호로 각각 $Δ x$ , $Δ y$ 와 같이 나타낸다. 즉, $Δ x = b - a$ $Δ y = f (b) - f (a) = f (a + Δ x) - f (a)$

Definition 8 (평균변화율(ARC or MV) : Average Rate of Change) $A R C (f, a, b) = M V (f, a, b) = \frac{Δ y}{Δ x} = \frac{f (b) - f (a)}{b - a} = \frac{f (a + Δ x) - f (a)}{Δ x}$

Definition 9 ( $x = a$ 에서의 미분계수, 순간변화율, IRC¹) $I R C (f, a) = f^{'} (a) = lim_{Δ x \to 0} \frac{f (a + Δ x) - f (a)}{Δ x} = lim_{x \to a} \frac{f (x) - f (a)}{x - a}$

$I R C (f, a) = f^{'} (a) = lim_{Δ x \to 0} A R C (f, a, a + Δ x)$

Definition 10 (미분가능한함수) 함수 $y = f (x)$ 가 어떤 구간에 속하는 모든 $x$ 에서 미분가능하면 함수 $y = f (x)$ 는 그 구간에서 미분가능하다고 한다.

특히 함수 $y = f (x)$ 가 정의역에 속하는 모든 $x$ 에서 미분가능하면 함수 $y = f (x)$ 는 미분가능한 함수라 한다.

Remark (연속 및 미분가능).

$f (x) \notin C^{0} (x = α)$
1. $(f (x) (x - α) \in C^{0} (x = α)) \land (f (x) \in C^{1} (x = α) \lor f (x) \notin C^{1} (x = α))$
2. $f (x) (x - α) (x - α) \in C^{1} (x = α)$
$f (x) \notin C^{1} (x = α)$
1. $f (x) \in C^{0} (x = α) \lor f (x) \notin C^{0} (x = α)$
2. $f (x) (x - α) (x - α) \in C^{1} (x = α)$

미분계수의 기하학적 의미

Remark (미분계수). $f^{'} (a)$ 는 곡선 $y = f (x)$ 위의 점 $P (a, f (a))$ 에서의 접선의 기울기와 같다.

미분가능성과 연속성

도함수와 미분법

Definition 11 (도함수-a derived function) 미분가능한 함수 $y = f (x)$ 의 정의역의 각 원소 $x$ 에 미분계수 $f^{'} (x)$ 를 대응시키면 새로운 함수 $f^{'} : X \to R, f^{'} (x) = lim_{Δ x \to 0} \frac{f (x + Δ x) - f (x)}{Δ x}$ 를 얻는다. 이 때 이 함수 $f^{'} (x)$ 를 함수 $f (x)$ 의 도함수라 하고, 이것을 기호로 $f^{'} (x), y^{'}, \frac{d y}{d x}, \frac{d}{d x} f (x)$ 로 나타낸다.

Definition 12 (미분법) 함수 $y = f (x)$ 에서 도함수 $f^{'} (x)$ 를 구하는 것을 함수 $y = f (x)$ 를 $x$ 에 대하여 미분한다고 하고, 그 계산법을 미분법이라 한다.

Theorem 12 (함수 $y = x^{n}$ (n은 양의 정수)과 상수함수의 도함수)

$y = x^{n}$ ( $n \in N$ )이면 $y^{'} = n x^{n - 1}$
$y = c$ (c는 상수)이면 $y^{'} = 0$

Theorem 13 (함수의 실수배, 합, 차, 곱의 미분법) 세 함수 f(x), g(x), h(x)가 미분가능할 때

${k f (x)}^{'} = k f^{'} (x)$ (단, k는 상수)
${f (x) + g (x)}^{'} = f^{'} (x) + g^{'} (x)$
${f (x) - g (x)}^{'} = f^{'} (x) - g^{'} (x)$
${f (x) g (x)}^{'} = f^{'} (x) g (x) + f (x) g^{'} (x)$
${f (x) g (x) h (x)}^{'} = f^{'} (x) g (x) h (x) + f (x) g^{'} (x) h (x) + f (x) g (x) h^{'} (x)$
$[{f (x)}^{n}]^{'} = n {f (x)}^{n - 1} f^{'} (x)$ (단, n은 양의 정수)

Theorem 14 (미분과나머지정리의관계)

이차 이상의 다항식 $f (x)$ 에서

$\begin{matrix} (2) & M o d (f (x), (x - a)^{2}) = f^{'} (a) (x - a) + f (a) \end{matrix}$

이차 이상의 다항식 $f (x)$ 에서

$\begin{matrix} (3) & M o d (f (x), (x - a)^{2}) = 0 ⟺ f (a) = 0, f^{'} (a) = 0 \end{matrix}$

Proof. Equation 2 의 경우

다항식 $f (x)$ 를 $(x - a)^{2}$ 으로 나누었을 때의 몫을 $Q (x)$ , 나머지를 $m x + n$ 이라 하면 $\begin{matrix} (4) & f (x) = (x - a)^{2} Q (x) + m x + n \end{matrix}$ Equation 4 의 양변을 $x$ 에 대하여 미분하면 $\begin{matrix} (5) & f^{'} (x) = 2 (x - a) Q (x) + (x - a)^{2} Q^{'} (x) + m \end{matrix}$ Equation 4 에 $x = a$ 를 대입하면 $f (a) = m a + n, 즉 n = f (a) - m a$ $f^{'} (a) = m$ $(???), (???)$ 에서 $mx+n=f’(a)x+f(a)-af’(a)=f’(a)(x-a)+f(a) $

의 경우

나누어 떨어지면 $m x + n = 0$ , 즉 $m = 0$ , $n = 0$ 이 되어야 하므로 (3), (4)에서 $f (a) = 0$ , $f^{'} (a) = 0$

Theorem 15 (기타)

$(e v e n f u n c t i o n)^{'} = (o d d f u n c t i o n)$ : 미분 정의대로 하면 증명은 쉽다.

image

Remark (역함수 미분법 참고).

역함수미분법

Theorem 16 (역함수의 미분법 - hakchin notation 1) 미분가능한 함수 $f (x)$ 의 역함수 $f^{- 1} (x) = g (x)$ 가 존재하고 미분가능할 때, $x = f^{- 1} (y) = g (y)$ 의 도함수는 다음과 같다. $\begin{aligned} g^{'} (y) \cdot f^{'} (x) & = 1 \\ g^{'} (x) \cdot f^{'} (y) & = 1 \end{aligned}$

Proof. $\begin{aligned} g (f (x)) = x & \Rightarrow (g (f (x)))^{'} = (x)^{'} \\ \Rightarrow g^{'} (f (x)) \cdot f^{'} (x) = 1 (w h e r e f^{'} (x) \neq 0) \end{aligned}$

Theorem 17 (역함수의 미분법 - hakchin notation2) 미분가능한 함수 f(x)의 역함수 $f^{- 1} (x) = g (x)$ 가 존재하고 미분가능할 때, $y = f^{- 1} (x)$ 의 도함수는 다음과 같다. $\begin{aligned} f^{'} (f^{- 1} (x)) \cdot (f^{- 1})^{'} (x) & = 1 (w h e r e f^{'} (f^{- 1} (x)) \neq 0) \\ f^{'} (y) \cdot (f^{- 1})^{'} (x) & = 1 (w h e r e f^{'} (f^{- 1} (x)) \neq 0) \end{aligned}$

$\begin{aligned} g^{'} (y) \cdot f^{'} (x) & = 1 \\ g^{'} (x) \cdot f^{'} (y) & = 1 \end{aligned}$

Proof. $\begin{aligned} f (f^{- 1} (x)) = x & \Rightarrow (f (f^{- 1} (x)))^{'} = (x)^{'} \\ \Rightarrow f^{'} (f^{- 1} (x)) \cdot (f^{- 1})^{'} (x) = 1 (w h e r e f^{'} (f^{- 1} (x)) \neq 0) \end{aligned}$

Theorem 18 (역함수의미분법) 미분가능한 함수 $f (x)$ 의 역함수 $f^{- 1} (x)$ 가 존재하고 미분가능할 때, $y = f^{- 1} (x)$ 의 도함수는 다음과 같다. $\begin{aligned} \frac{d y}{d x} & = \frac{1}{\frac{d x}{d y}} o r \\ (f^{- 1})^{'} (x) & = \frac{1}{f^{'} (y)} (w h e r e f^{'} (y) \neq 0) \end{aligned}$

Proof. $\begin{aligned} f (f^{- 1} (x)) = x & \Rightarrow f^{'} (f^{- 1} (x)) ((f^{- 1})^{'} (x)) = 1 \\ \Rightarrow (f^{- 1})^{'} (x) = \frac{1}{f^{'} (f^{- 1} (x))} = \frac{1}{f^{'} ()} \end{aligned}$

$\begin{aligned} y = f^{- 1} (x) & \Rightarrow x = f (y) \\ \Rightarrow \frac{d y}{d x} = (f^{- 1})^{'} (x), \frac{d x}{d y} = f^{'} (y) \end{aligned}$

$\begin{array}{r} ∴ \frac{d y}{d x} = \frac{1}{f^{'} (y)} = \frac{1}{\frac{d y}{d x}} (w h e r e f^{'} (y) \neq 0) \end{array}$

함수 $y = f^{- 1} (x)$ 에서 $x = f (y)$ 이고 $\frac{d x}{d y} = f^{'} (y)$ 이다. $x = f (y)$ 의 양변을 $x$ 에 대하여 미분하면 $\frac{d}{d x} (x) = \frac{d}{d x} (f (y)), 1 = \frac{d}{d y} (f (y)) \cdot \frac{d y}{d x} = f^{'} (y) \cdot \frac{d y}{d x}$ $∴ \frac{d y}{d x} = \frac{1}{f^{'} (y)} = \frac{1}{\frac{d y}{d x}} (w h e r e f^{'} (y) \neq 0)$ :::

Exercise 1 (역함수의 미분법) 미분가능한 함수 $f (x)$ 의 역함수를 $g (x)$ , $f (3 x - 5)$ 의 역함수를 $(x)$ 라 할 때, $h^{'} (x)$ 를 $g^{'} (x)$ 로 나타내면?

Solution. $g (x) = f^{- 1} (x) \Rightarrow f (g (x)) = x$

$\begin{aligned} h (x) = (f (3 x - 5))^{- 1} & \Rightarrow f (3 x - 5) (h (x)) = x \\ \Rightarrow f (3 h (x) - 5) = x \end{aligned}$ 이므로 $g (x) = 3 h (x) - 5$ 이고 이것의 양변을 미분하면 $g^{'} (x) = 3 h^{'} (x) \Rightarrow h^{'} (x) = \frac{1}{3} g^{'} (x)$

도함수의 활용

접선의 방정식과 평균값 정리

Theorem 19 (Rolle’s theorem) $f \in C^{0} ([a, b]) \land f \in C^{1} ((a, b)) \land f (a) = f (b) \Rightarrow \exists c \in (a, b) (f^{'} (c) = 0)$

Theorem 20 (Rolle’s theorem ww) If $f : [a, b] \to R$ is a continuous function, differentiable on the open interval $(a, b)$ , and $f (a) = f (b)$ , then there exists at least one c in the open interval $(a, b)$ such that $f^{'} (c) = 0$

This version of Rolle’s theorem is used to prove the mean value theorem, of which Rolle’s theorem is indeed a special case. It is also the basis for the proof of Taylor’s theorem.

Theorem 21 (MVT) $f \in C^{0} ([a, b], R) \land f \in C^{1} ((a, b), R) \Rightarrow \exists c \in (a, b) (f^{'} (c) = \frac{f (b) - f (a)}{b - a})$

Theorem 22 (MVT-다른표기) $f \in C^{0} ([a, b]) \land f \in C^{1} ((a, b)) \Rightarrow \exists c \in (a, b) (f^{'} (c) = A R C (f, a, b) = M V (f, a, b)$

Theorem 23 (평균값 정리(MVT) Let $f : [a, b] \to R$ be a continuous function, and differentiable on the open interval $(a, b)$ , where $a < b$ . Then there exists some $c$ in $(a, b)$ such that $f^{'} (c) = \frac{f (b) - f (a)}{b - a}$

Example 1 (이차함수관련) 이차함수 $f (x)$ 에 대하여 $f^{'} (\frac{a + b}{2}) = \frac{f (b) - f (a)}{b - a}$

함수의 증가와 감소

Remark (notation idea for increasing). 다음을 참고하였다.

Shorthand notation for "increases" and"decreases"

Definition 13 (증가함수) $f \in \ddot{I} (R) ⟺ x_{1} < x_{2} \Rightarrow f (x_{1}) < f (x_{2})$

Definition 14 (감소함수) $f \in - \ddot{I} (R) ⟺ x_{1} < x_{2} \Rightarrow f (x_{1}) > f (x_{2})$

Definition 15 (증가상태) $\forall ε > 0, \exists δ, 0 < δ < ε \Rightarrow f (a - δ) < f (a) < f (a + δ) ⟺$ $f (x)$ 는 $x = a$ 에서 증가상태에 있다고 한다.

Definition 16 (감소상태) $\forall ε > 0, \exists δ, 0 < δ < ε \Rightarrow f (a - δ) > f (a) > f (a + δ) ⟺$ $f (x)$ 는 $x = a$ 에서 감소상태에 있다고 한다.

Theorem 24 (함수의증가1) $f \in C^{1} ((a, b)) \land (\forall x \in (a, b)) (f^{'} (x) > 0) \Rightarrow f \in \ddot{I} ((a, b))$

Theorem 25 (함수의감소1) $f \in C^{1} ((a, b)) \land (\forall x \in (a, b)) (f^{'} (x) < 0) \Rightarrow f \in - \ddot{I} ((a, b))$

Theorem 26 (함수의 증가2) $f \in C^{1} ((a, b)) \land f 는 증가상태 \land (\forall x \in (a, b)) (f^{'} (x) \geq 0) \Rightarrow f \in \ddot{I} ((a, b))$

Theorem 27 (함수의 감소2) $f \in C^{1} ((a, b)) \land f 는 감소상태 \land (\forall x \in (a, b)) (f^{'} (x) \leq 0) \Rightarrow f \in - \ddot{I} ((a, b))$

Theorem 28 (함수의증가3) $f \in C^{1} ((a, b)) \land f \in \ddot{I} ((a, b)) \Rightarrow f^{'} (x) \geq 0$

Theorem 29 (함수의감소3) $f \in C^{1} (I) \land f \in - \ddot{I} (I) \Rightarrow f^{'} (x) \leq 0$

함수의 극대와 극소

Definition 17 (임계점, critical point) $a \in D o m (f) \land a$ is a critical point $⟺ f^{'} (a) = 0 \lor f^{'} (a)$ does not exist.

Remark (Extrema & Critical point). 극값을 갖는다 $\overset{O}{\underset{X}{⇄}}$ 임계값을 갖는다.

Definition 18 (극대, local Maximum) 함수 $f (x)$ 가 $x = a$ 에서 연속이고 $x = a$ 의 좌우에서 $f (x)$ 가 증가상태에서 감소상태로 바뀔 때, $f (x)$ 는 $x = a$ 에서 극대라 하며, $f (a)$ 를 극댓값이라 한다.

Definition 19 (극대, local Maximum kk) $lim_{x \to a} f (x) = f (a) \land \exists h > 0, \forall x \in (a - h, a + h), f (a) \geq f (x)$ 이면 $f (x)$ 는 $x = a$ 에서 극대라 하며, $f (a)$ 를 극댓값이라 한다.

Definition 20 (엄격한 극대, strict local Maximum) $lim_{x \to a} f (x) = f (a) \land \exists h > 0, \forall x \in (a - h, a + h) - {a}, f (a) > f (x)$ 이면 $f (x)$ 는 $x = a$ 에서 엄격한 극대라 하며, $f (a)$ 를 엄격한 극댓값이라 한다.

Definition 21 (엄격한 극대2, strict local Maximum2) $lim_{x \to a} f (x) = f (a) \land \forall h \in R - {0}, f (a + h) < f (a)$ 이면 $f (x)$ 는 $x = a$ 에서 엄격한 극대라 하며, $f (a)$ 를 엄격한 극댓값이라 한다.

Definition 22 (극소, local minimum) 함수 $f (x)$ 가 $x = a$ 에서 연속이고 $x = a$ 의 좌우에서 $f (x)$ 가 감소상태에서 증가상태로 바뀔 때, $f (x)$ 는 $x = a$ 에서 극소라 하며, $f (a)$ 를 극솟값이라 한다.

Definition 23 (극소, local minimum ee) $lim_{x \to a} f (x) = f (a) \land \exists h > 0, \forall x \in (a - h, a + h), f (a) \leq f (x)$ 이면 $f (x)$ 는 $x = a$ 에서 극소라 하며, $f (a)$ 를 극솟값이라 한다.

Definition 24 (엄격한 극소, strict local minimum) $lim_{x \to a} f (x) = f (a) \land \exists h > 0, \forall x \in (a - h, a + h) - {a}, f (a) < f (x)$ 이면 $f (x)$ 는 $x = a$ 에서 엄격한 극소라 하며, $f (a)$ 를 엄격한 극솟값이라 한다.

Definition 25 (엄격한극대2, strict local Maximum2) $lim_{x \to a} f (x) = f (a) \land \forall h \in R - {0}, f (a + h) < f (a)$ 이면 $f (x)$ 는 $x = a$ 에서 엄격한 극대라 하며, $f (a)$ 를 엄격한 극댓값이라 한다.

Theorem 30 (극값과 미분계수) 함수 $f (x)$ 가 $x = a$ 에서 극값을 가지고 $a$ 를 포함하는 어떤 열림구간에서 미분가능하면 $f^{'} (a) = 0$ 이다.

Remark. 일반적으로 위의 역은 성립하지 않는다.

Theorem 31 (극대관련) 미분가능한 함수 $f (x)$ 에서 $f^{'} (a) = 0$ 이고, $x = a$ 의 좌우에서 $f^{'} (x)$ 의 부호가 양에서 음으로 바뀌면 $f (x)$ 는 $x = a$ 에서 극대이고, 극댓값은 $f (a)$ 이다. (극댓값이라 하여 항상 $f^{'} (a) = 0$ 이 되는 것은 아니다. 즉, 미분가능하지 않은 연속함수의 경우)

Theorem 32 (극소관련) 미분가능한 함수 $f (x)$ 에서 $f^{'} (a) = 0$ 이고, $x = a$ 의 좌우에서 $f^{'} (x)$ 의 부호가 음에서 양으로 바뀌면 $f (x)$ 는 $x = a$ 에서 극소이고, 극솟값은 $f (a)$ 이다. (극솟값이라 하여 항상 $f^{'} (a) = 0$ 이 되는 것은 아니다. 즉, 미분가능하지 않은 연속함수의 경우)

Theorem 33 ( $f (x)$ 가 극값을 갖는 조건) $f (x) 가 극값 갖는다. \land f^{'} (x) 가 2차 함수 \Rightarrow f (x) = 0 은 서로 다른 2개 이상의 실근을 갖는다.$

Remark (상수함수). 어떤 열린 구간에서 극댓값이면서 극솟값이면 해당 구간에서 상수함수이다.

Remark (삼차함수사차함수대칭관계).

방정식과 부등식, 속도와 가속도

여러 가지 미분법

아래 위키를 참고하기

Remark.

역함수 미분법

Theorem 34

$y = \sin x \Rightarrow y^{'} = \cos x$
$y = \cos x \Rightarrow y^{'} = - \sin x$
$y = \tan x \Rightarrow y^{'} = \sec^{2} x$
$y = \csc x \Rightarrow y^{'} = - \csc x \cot x$
$y = \sec x \Rightarrow y^{'} = \sec x \tan x$
$y = \cot x \Rightarrow y^{'} = - \csc^{2} x$

Remark. 삼각함수 6각형을 보고 마음속으로 관련있는 공식들을 상기하여 보자.

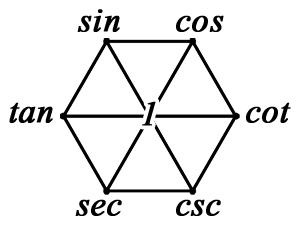
생각할 수 있는 것들은 일단 아래와 같은 것들이 있다.

삼각함수의 역수 관계
삼각함수의 제곱합 관계
삼각함수의 곱셈 관계
삼각함수의 미분 관계
쌍곡선함수(Hyperbolic function)의 미분 관계

로그함수의 미분법

Theorem 35 (로그함수의미분법) $y = f (x) \Rightarrow \frac{y^{'}}{y} = \frac{f^{'} (x)}{f (x)}$

Proof. $\begin{aligned} \Rightarrow | y | = | f (x) | \\ \Rightarrow l n | y | = l n | f (x) | \\ \Rightarrow \frac{y^{'}}{y} = \frac{f^{'} (x)}{f (x)} 양변을 x 에 대하여 미분한다 \end{aligned}$

삼각함수의 미분

개쎈 p572를 latex 으로 여기에 서술해 보기

$\begin{aligned} △ A B C & = 4 \\ △ A B C & = 5 \\ △ A B C & = 6 \\ △ A B C & = 7 \\ ▴ A B C & = 8 \end{aligned}$

Theorem 36 ( $\frac{s i n x}{x}$ 극한) blah,blah,blah,…

Proof. Insert related imaage later.

$△ O A P < Sector (O A P) < △ O A T$

접선의 방정식

Definition 26 곡선 위의 점 P에 대하여 곡선 위를 움직이는 점 Q가 P에 한없이 다가갈 때 직선 PQ가 하나의 직선으로 수렴한다면 그 극한 위치의 직선을 P에서의 접선이라 한다.

함수의 그래프

Definition 27 함수 $f (x)$ 위에 서로 다른 두 점을 잡았을 때, 두 점 사이의 독립변수에 대한 함수값이 두 점을 이은 선분보다 아래쪽의 값인 함수 즉, $\forall x_{1} \neq x_{2}, f (\frac{x_{1} + x_{2}}{2}) < \frac{f (x_{1}) + f (x_{2})}{2}$

Definition 28 함수 $f (x)$ 위에 서로 다른 두 점을 잡았을 때, 두 점 사이의 독립변수에 대한 함수값이 두 점을 이은 선분보다 위쪽의 값인 함수 즉, $\forall x_{1} \neq x_{2}, f (\frac{x_{1} + x_{2}}{2}) > \frac{f (x_{1}) + f (x_{2})}{2}$

Definition 29 Let $f (x)$ be a differentiable function on an interval $I$ . We will say that the graph of $f (x)$ is concave up on I $⟺ f^{'} (x)$ is increasing on I $⟺ f^{'} (x) 는 상수함수가 아니고 \land f^{″} (x) \geq 0$ .

Definition 30 Let $f (x)$ be a differentiable function on an interval$ I$ . We will say that the graph of $f (x)$ is concave down on I $⟺ f^{'} (x)$ is decreasing on $I$ $⟺ f^{'} (x) 는 상수함수가 아니고 \land f^{″} (x) \leq 0$ .

Theorem 37

$f^{'} (x) > 0 \Rightarrow f (x)$ 는 증가함수
$f (x) 는 상수함수가 아니고 \land f^{'} (x) \geq 0 ⟺ f (x)$ 는 증가함수
$f (x)$ 는 증가함수 $\Rightarrow f^{'} (x) \geq 0$
$f^{″} (x) > 0 \Rightarrow f (x) 는 위로 오목$
$f^{'} (x) 는 상수함수가 아니고 \land f^{″} (x) \geq 0 ⟺ (f^{'} (x) 는 증가함수) ⟺ f (x) 는 위로 오목$
$f (x) 는 이 구간에서 위로 오목 \Rightarrow f^{″} (x) \geq 0$

Definition 31 곡선 $y = f (x)$ 위의 점 $P (a, f (a))$ 에 대하여 $x = a$ 의 좌우에서 곡선의 모양이 아래로 오목에서 위로 오목으로 바뀌거나 위로 오목에서 아래로 오목으로 바뀔 때 이 점 $P$ 를 곡선 $y = f (x)$ 의 변곡점이라 한다. 따라서 변곡점 $P (a, f (a))$ 의 좌우에서 $f^{″} (x)$ 의 부호가 바뀌므로 $f^{″} (a)$ 가 존재하면 $f^{″} (a) = 0$ 이다.

Theorem 38 함수 $y = f (x)$ 에 대하여 $f^{″} (a) = 0$ 이고, $x = a$ 의 좌우에서 $f^{″} (x)$ 의 부호가 바뀌면 점 $(a, f (a))$ 는 곡선 $y = f (x)$ 의 변곡점이다. (변곡점이라 하여 항상 $f^{″} (a) = 0$ 이 되는 것은 아니다. 즉, 미분가능하지 않은 연속함수의 경우)

Remark. If a function has a second derivative, the value of the second derivative is either 0 or undefined at each of that function’s inflection points.

적분

부정적분

Definition 32 (부정적분1) 미분하여 $f (x)$ 가 되는 함수를 $f (x)$ 의 부정적분 또는 원시함수라고 한다. 이 함수를 기호로 $\int f (x) d x$ 로 나타낸다. 즉, $\frac{d}{d x} \int f (x) d x = f (x)$ 이다. 함수 $f (x)$ 의 부정적분은 하나로 정해지지 않는다. 이 때, $f (x)$ 의 알려진 부정적분중의 하나가 $f (x)$ 라면, $f (x)$ 의 임의의 부정적분은 $f (x) + C$ 의 꼴로 나타내어지며, $\int f (x) d x = F (x) + C (w h e r e C i s a c o n s t a n t)$ 이다. 여기에서 $\int$ 를 integral symbol, $c$ 를 적분상수(the constant of integration), 함수 $f (x)$ 를 피적분함수(the integrand), $x$ 를 적분변수(the integration variable)라 하고, $f (x)$ 의 부정적분을 구하는 것을 $f (x)$ 를 적분한다라고 한다.

Theorem 39 (부정적분표현) $(F (x))^{'} = f (x) \Rightarrow \int f (x) = F (x) + C$

Proof. $\begin{aligned} (\int f (x) d x - F (x))^{'} = f (x) - f (x) = 0 \\ \Rightarrow \int f (x) d x - F (x) = C \\ \Rightarrow \int f (x) d x = F (x) C \end{aligned}$

Theorem 40 (함수의 실수배, 합, 차의 부정적분) 두 함수 $f (x), g (x)$ 가 부정적분을 가질 때

$\int k f (x) d x = k \int f (x) d x$ (단, k는 0이 아닌 상수)
$\int {f (x) \pm g (x)} d x = \int f (x) d x \pm \int g (x) d x$

Reference Sites

삼각함수적분-COS편

정적분

Definition 33 (정적분 dd) $\int_{a}^{b} f (x) d x = lim_{n \to \infty} \sum_{k = 1}^{n} f (x_{k}) Δ_{x} (w h e r e Δ x = \frac{b - a}{n}, x_{k} = a + Δ x \cdot k)$

Theorem 41 (급수와 정적분의 관계) $lim_{n \to \infty} \sum_{k = 1}^{n} f (a + \frac{p k}{n}) \cdot \frac{q}{n} = q \int_{0}^{1} f (a + p x) d x = \frac{q}{p} \int_{0}^{p} f (a + x) d x$

Proof.

You can use Definition of definite integral 과 평행이동 or $\frac{p k}{n} = x$ and $\frac{p}{n} = d x$ . 이 때 위 끝은 k 대신에 n을 대입하고 $\infty$ 하면 p 이고 아래 끝은 k 대신에 1을 대입하고 $\infty$ 하면 0 이 된다.

Proof.

다른 관점으로 생각해 본다면, $\frac{p k}{n} = x_{k}$ and $\frac{p}{n} = Δ x$ 라고 생각해도 되겠다. 그리고 정적분의 정의를 잘 생각해 본다.

Remark (급수와정적분의관계). $\begin{aligned} \int_{a}^{b} f (x) d x & = \int_{0}^{b - a} f (x + a) d x \\ = (b - a) \int_{0}^{1} f ((b - a) x + a) d x \end{aligned}$

Theorem 42 (부분적분법) $\int f (x) g^{'} (x) d x = f (x) g (x) - \int f^{'} (x) g (x) d x$

Proof. 어쩌구 저쩌구

Remark (tabular integration). tabular integration 이라는 방법을 쓰면 좀 쉽게 할 수 있다. youtube 자료로는 https://youtu.be/E8N1E5ZAiIU 찾아볼 수 있다.

Example 2 (부분적분법 dd) 미분가능한 두 함수 $f (x)$ , $g (x)$ 가 구간 $[a, b]$ 에서 $f^{'} (x) = \frac{1}{4} g (x)$ 를 만족할 때, 다음 중 정적분 $\int_{a}^{b} f (x) g (x) d x$ 와 같은 것은?

Solution. $2 [{f (b)}^{2} - {f (a)}^{2}]$

Remark (삼차함수넓이적분).

다항함수 넓이 공식
삼차함수의 넓이
$\int_{α}^{β} a (x - α) (x - β) (x - γ) d x = \frac{a}{6} (β - α)^{3} (γ - \frac{α + β}{2})$

정적분의 활용

속도와 거리

Remark (위치·속도·가속도의관계). 위치를 미분하면 속도, 속도를 미분하면 가속도를 구할 수 있고, 미분과 적분은 서로 역연 산의 관계이므로 다음이 성립한다.

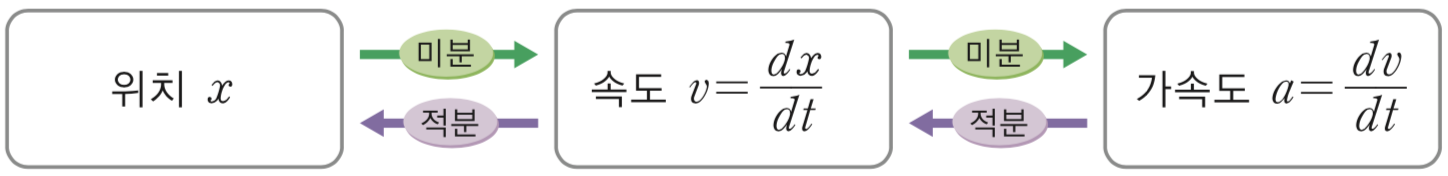
Theorem 43 (속도와거리) 수직선 위를 움직이는 점 $P$ 의 시각 $t$ 에서의 위치를 $l = l (t)$ 라 하면, 그 때의 속도는 $v (t) = \frac{d l}{d t} = l^{'} (t)$ 이다.

점 $P$ 의 위치 (시각 $t$ )
$l (t) = l (t_{0}) (= l_{0}) + \int_{t_{0}}^{t} v (x) d x$
점 $P$ 의 위치의 변화량 ( $t = a \to t = b$ )
$l (b) - l (a) = \int_{a}^{b} v (t) d t$
점 $P$ 의 실제로 움직인 거리 ( $t = a \to t = b$ )
$s = \int_{a}^{b} | v (t) | d t$

Footnotes

Instantaneous Rate of Change↩︎